알고리즘 분류 : 수학, 기하학, 볼록 껍질, 분할 정복

입력으로 원들의 중심좌표와 반지름이 주어질 때
모든 원들을 감싸는 끈의 최소 길이를 구해야 한다.
(원과 원 사이는 직선으로 감싸야 한다)


일반적인 컨벡스 헐 알고리즘은 점들을 이어 볼록 다각형을 만들지만
해당 문제는 원이라서 크기에 따라서 재방문 가능하기 때문에 그래프로 접근했다.
하나의 케이스에 최대 100개의 원이 주어지기 때문에
모든 원들에 대해 서로 다른 원과의 접선의 기울기를 구해도 시간내에 연산이 가능하다.
각각의 원에 대해서 다른 모든 원과의 외접선의 기울기를 알고 있다면
직전에 선택된 접선과 반시계 방향이면서 각의 차이가 가장 작은 외접선을 찾으면 된다.
첫번째 원부터 외접선의 기울기가 가장 작은 원을 찾아 위 과정을 반복한다.
이미 사용한 외접선을 또 방문한 경우 탐색을 종료한다.
첫번째 원이 둘레에 포함되어야지만 성립이 되기 때문에
(y좌표 - 반지름)을 기준으로 오름차순 정렬하고 첫번째 원부터 탐색한다.
두 원의 외접선의 기울기는 다음과 같이 구할 수 있다.

(a) arctan( 두 원의 중심점을 잇는 직선의 기울기 )
double tan(circle a, circle b) {
double dx = b.x - a.x, dy = b.y - a.y;
if (dx == 0) {
if (dy < 0) return 1.5 * pi;
return 0.5 * pi;
}
if (dy == 0) {
if (dx < 0) return pi;
return 0;
}
double tang = atan(dy / dx);
if (dx < 0) return pi + tang;
if (dy > 0) return tang;
return 2 * pi + tang;
}tan(α) = dy / dx
α = arctan( tan(α) )
(b) arcsin( (두 원의 반지름의 차) / (두 원의 중심점의 거리) )
sin(β) = dr / sqrt( pow(dx, 2) + pow(dy, 2) )
β = arcsin( sin(β) )
double tanh(circle a, circle b) {
double t = tan(a, b);
t -= asin((b.r - a.r) / dis(a, b));
if (t >= 2 * pi) t -= 2 * pi;
if (t < 0) t += 2 * pi;
return t;
}두 원의 외접선의 기울기 = α + β
호의 길이와 외접선의 길이는 다음과 같이 구할 수 있다.
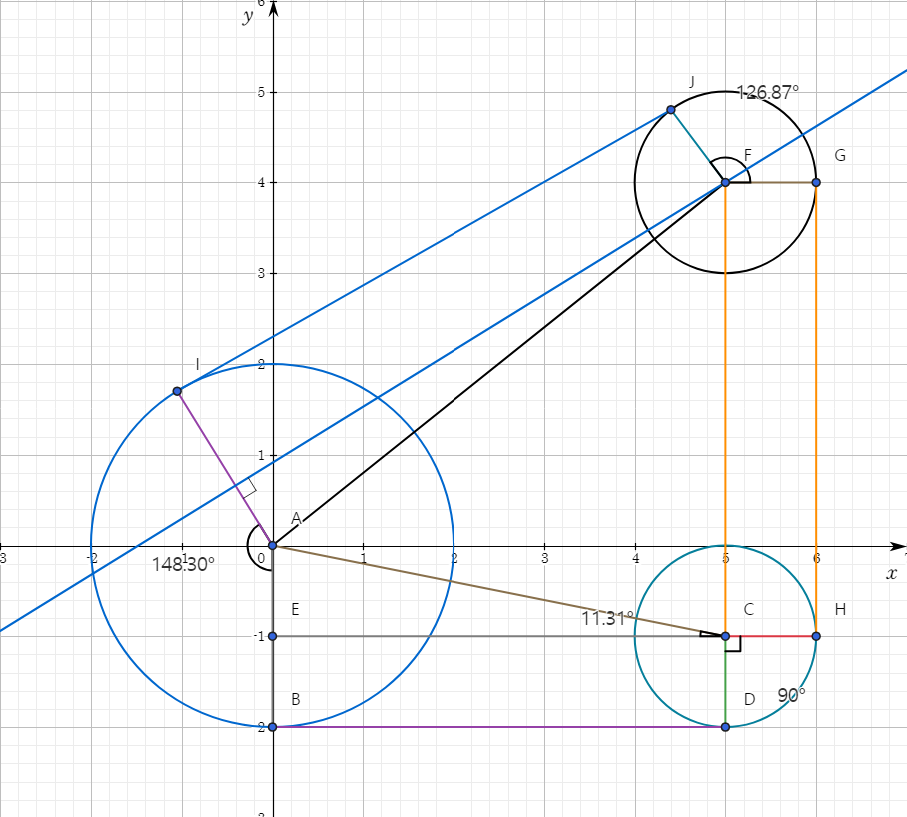
호의 길이는 (인접한 외접선들의 기울기 각 차이 * 원의 반지름)으로 구할 수 있고
외접선의 길이는 피타고라스 정리로 구할 수 있다.
둘러싼 모든 외접선과 호의 길이를 구하면 정답을 구할 수 있다.
'컴퓨터공학 > PS' 카테고리의 다른 글
| BOJ 1759 암호 만들기 (0) | 2023.07.13 |
|---|---|
| BOJ 15086 Craters (0) | 2023.07.10 |
| BOJ 3970 안전 구역 (0) | 2023.07.10 |